Mit Sicherheit ist dir im Unterricht schon einmal aufgefallen, dass nicht alle Funktionen gleich aussehen und dass viele Funktionen spezielle Punkte aufweisen. Man könnte auch sagen, jede Funktion hat ihre eigenen Merkmale, an denen man erkennt, dass es sich genau um diese Funktion handeln muss. Beispiele für diese Merkmale sind Hoch oder Tiefpunkte, Nullstellen, Wendestellen oder auch die Monotonie einer Funktion. Sagt dir alles noch nichts? Kein Problem! In diesem Blogbeitrag wird dir einfach und schnell erklärt wie du die Merkmale einer Funktion erkennst und welche Auswirkungen sie auf die Funktion haben.
Beginnen wir mit Hoch und Tiefpunkten und mit den Nullstellen:
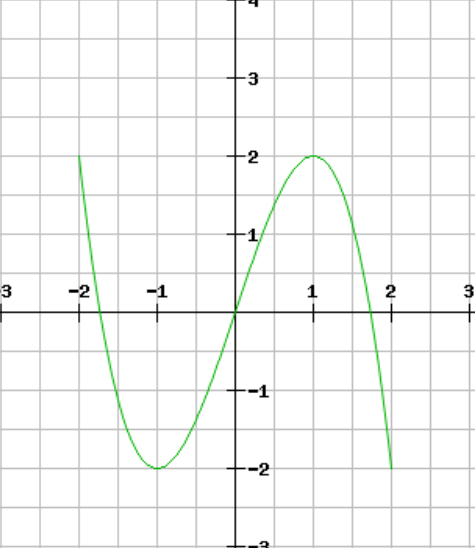
Hier siehst du ein einfaches Beispiel für einen Hoch bzw Tiefpunkt. Diese erkennst du in einem Graphen sehr leicht, da die Steigung an diesen Punkten Null sein muss, also f´(x)=0. In unserem Beispiel wäre dies bei x= -1 und bei x=1 der Fall.
Nullstellen sind vorhanden wenn unsere Funktion die x-Achse schneidet, also hier ungefähr bei x=-1,8, x=0 und x=1,8. Bei einer Nullstelle muss der passende y-Wert Null sein, zum Beispiel f(1,8)=0.
Eine Wendestelle ist immer dann vorhanden, wenn sich die Krümmung der Funktion ändert. Also zum Beispiel von einer Rechtskrümmung zu einer Linkskrümmung. Dieser Punkt ist immer dort, wo die Steigung des Graphen am stärksten/schwächsten ist. In unserer Funktion wäre eine Wendestelle ungefähr bei x= 0,5. Stell dir vor du fährst mit dem Fahrrad die Funktion entlang. Du startest bei x=0. Genau an der Wendestelle müsstest du in die andere Richtung lenken, also erkennst du einen Krümmungswechseln und somit auch deine Wendestelle. Für Wendestellen gilt f´´(x)= 0 und f´´´(x) darf nicht 0 ergeben.
Die Monotonie eines Graphen erkennst du auch sehr leicht. Ist eine Funktion durchgehend steigend, dann ist sie streng monoton steigend. Das gleiche gilt andersherum, also wenn eine Funktion durchgehend fällt, so ist diese streng monoton fallend. Bei str. mon. steigenden Funktionen ist die Ableitung positiv und bei str. mon. fallenden Funktionen ist diese negativ.
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.