Monotonie einer Funktion

Nun besprecht ihr im Matheunterricht schon etwas länger die verschiedenen Merkmale einer Funktion und wie sie überprüft werden können. Du bist dir in allen Bereichen sicher, doch die Monotonie fällt dir noch etwas schwer? Kein Problem, in diesem Blogbeitrag wird dir alles Wichtige zur Monotonie erklärt und danach wirst du mit Sicherheit alles besser verstehen.

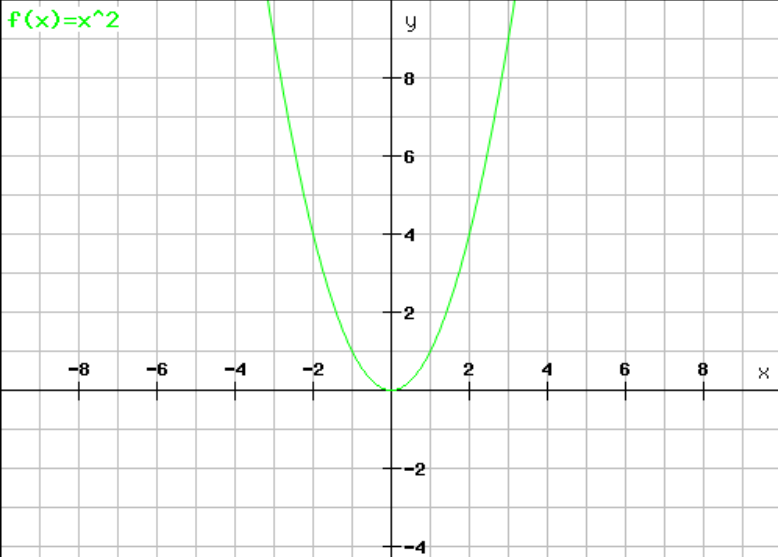
Teilen wir unsere Funktion f(x)= x² in zwei Intervalle. Einmal I (-2|0) und I(0|2).

I (-2|0): Dieses Intervall ist str. mon. fallend, da für alle x auf unserem Intervall  gilt: f(x1) > f(x2). Die negative Steigung verdeutlicht dies, je weiter links der Punkt in unserem Intervall liegt desto größer ist der passende y-Wert.

I(0|2): Dieses Intervall ist str. mon.  wachsend, da für alle x auf unserem Intervall gilt: f(x1) < f(x2). Die positive Steigung verdeutlicht dies und je weiter rechts der Punkt auf unserem Intervall liegt, desto größer ist der passende y-Wert. [/av_textblock] [av_hr class='invisible' height='15' shadow='no-shadow' position='center' custom_border='av-border-thin' custom_width='50px' custom_border_color='' custom_margin_top='30px' custom_margin_bottom='30px' icon_select='yes' custom_icon_color='' icon='ue808' font='entypo-fontello' av_uid='av-lwqxjz'] [av_textblock size='' font_color='' color='' av_uid='av-l4duan'] Nun fragst du dich mit Sicherheit wie man denn jetzt die Monotonie nachweisen kann. Wir suchen hierfür ein neues Beispiel und gehen Schritt für Schritt vor:

Beispiel: f(x)= 4x² + 7

Schritt 1: Ableiten →  f´(x)= 8x

Schritt 2: Für x einmal eine möglichst große  und möglichst kleine Zahl einsetzten und die Ergebnisse vergleichen.

→ f‘(1)= 8⦁1= 8

→ f‘(1000)= 8⦁1000= 8000

⇒ Wir erkennen nun, dass unser zweites Ergebnis deutlich größer ist und somit gilt: f(x1) <  f(x2), das heißt unsere Funktion ist str. mon. wachsend.

Kurze Erklärung: Um bei einer Funktion eine Monotonie nachweisen zu können, musst du sie als erstes immer ableiten. Dann setzt du in die Ableitung einen großen und einen kleinen x-Wert ein. Bei dem kleinen x-Wert muss der y-Wert auch klein sein, bei dem großen x-Wert muss der y-Wert auch groß sein. Bei einer streng monoton steigenden Funktion gilt dann f(x1) <  f(x2) und bei einer streng monoton fallenden muss gelten:  f(x1) > f(x2).