Genauso wie Buchstaben zu den Grundlagen des Deutsch-Unterrichts gehören, so ist der gekonnte Umgang mit Brüchen die Basis für deinen Erfolg beim Mathe lernen. In diesem Blogbeitrag werden wir daher die wichtigsten Grundlagen für das sichere Bruchrechnen schaffen und uns mit der Addition (also dem Plusrechnen) beschäftigen.
Online-Nachhilfe
Erhalte Online-Nachhilfeunterricht von geprüften Nachhilfelehrern mithilfe digitaler Medien über Notebook, PC, Tablet oder Smartphone.
✓ Lernen in gewohnter Umgebung
✓ Qualifizierte Nachhilfelehrer
✓ Alle Schulfächer
✓ Flexible Vertragslaufzeit
Rechnen mit Brüchen – Die Grundlagen
Was ist ein Bruch? – Erklärung am Beispiel eines Kuchen
Oftmals essen wir in unserem Alltag nur einen Teil von einem Ganzen (Beispiel: ein halbes Brötchen, eine Viertel Piza …). Mit Brüchen können wir diese Anteile von einem Ganzen mathematisch aufschreiben.
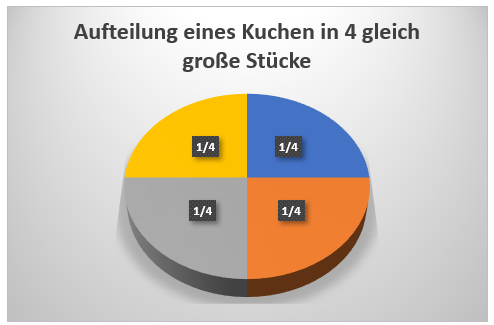
Wenn man einen Kuchen in 4 gleich große Teile teilt, so ist jedes Teil ein Viertel des Kuchens groß.
Angenommen wir essen ein Kuchenstück von insgesamt 4 Stücken. Mathematisch können wir das mit diesem Bruch aufschreiben:
![]()
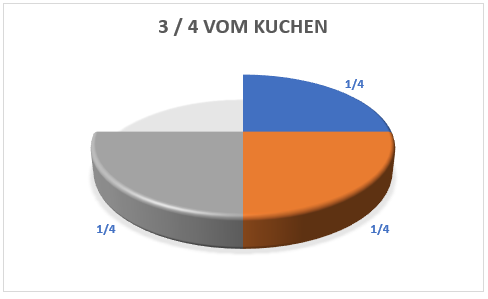
Wenn wir ein Kuchenstück essen, bleiben 3 von insgesamt 4 Kuchenstücken übrig.
In einem Bruch ausgedrückt können wir sagen: „Drei Viertel des Kuchens sind noch übrig“
Wir schreiben:
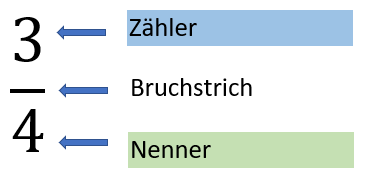
Ein Bruch wird in der „Zähler-Bruchstrich-Nenner-Schreibweise“ angegeben. Dies bedeutet, dass oberhalb vom Bruchstrich immer der Zähler steht und unterhalb vom Bruchstrich immer der Nenner.
Die Zahl unter dem Bruchstrich (der Nenner) gibt an, in wie viele Teile das ganze geteilt wird. Im Beispiel des Kuchens ist der Nenner 4, weil der Kuchen in 4 gleich große Teile (Kuchenstücke) geschnitten wird.
Die Zahl über dem Bruchstrich (der Zähler) gibt an, wie viele Teile gemeint sind. In unserem Beispiel wurde nur ein Kuchenstück gegessen. Es bleiben also 3 Kuchenstücke übrig. Also schreiben wir die Zahl 3 als Zähler.
Der Bruchstrich zwischen Zähler und Nenner gibt bei unserem Beispiel an, dass 3 von 4 Kuchenstücken übrigbleiben.
Wie groß ist ein Bruch – 3 Merkregeln
Diese 3 Merkregeln musst du beim Bruchrechnen wissen
Merkregel 1:
Ist der Zähler kleiner als der Nenner, so ist der Bruch immer kleiner als 1:
Zähler < Nenner → Bruch < 1
Beispiel: Beim Bruch 1/2 ist der Zähler 1 und der Nenner 2. Der Bruch muss also kleiner als 1 sein. Es gilt: 1/2 = 0,5 < 1
Merkregel 2:
Ist der Zähler gleich groß wie der Nenner, so ist der Bruch genau 1:
Zähler = Nenner → Bruch = 1
Beispiel: Beim Bruch 6/6 ist der Zähler 6 und der Nenner 6. Der Bruch ist also genau 1. Es gilt also: 6/6 = 1/1 = 1
Merkregel 1:
Ist der Zähler kleiner als der Nenner, so ist der Bruch größer als 1:
Zähler > Nenner → Bruch > 1
Beispiel: Beim Bruch 3/2 ist der Zähler 3 und der Nenner 2. Der Bruch muss also größer als 1 sein. Es gilt: 3/2 = 1,5 > 1
Die 4 Grundrechenarten:
Erfahre, wie man die Grundrechenarten bei Brüchen einsetzt
Mit Brüchen kann man die 4 Grundrechenarten ausführen:
- Addition (+)
- Subtraktion (-)
- Multiplikation (•)
- Division (:)
Addieren von Brüchen
Erfahre alles zur Addition von Brüchen
Brüche zu addieren bedeutet, dass verschiedene Brüche mit dem Vorzeichen + zusammengerechnet werden.

3 Schritte zur Addition von Brüchen
Erfahre, wie die 3-Schritt-Methode funktioniert
Beim Addieren von Brüchen gehen wir immer nach der 3-Schritt-Methode vor:
1. Schritt: Wir suchen den kleinsten gemeinsamen Nenner (Erweitern)
Um Brüche addieren zu können, müssen wir immer zunächst einen gemeinsamen Nenner finden.
Im Beispiel oben haben wir beim Bruch 1/2 den Nenner 2 und beim Bruch 2/3 den Nenner 3. Der kleinste gemeinsame Nenner von 2 und 3 ist die Zahl 6.

Wir müssen die beide Brüche so erweitern, dass im Nenner die Zahl 6 (also der kleinste gemeinsame Nenner) steht.
Merke: Wir erweitern einen Bruch, indem der Nenner und der Zähler mit derselben Zahl multipliziert werden.
Um 6 als gemeinsamen Nenner zu erhalten, müssen wir den Bruch 1/2 mit 3 erweitern:

Den Bruch 2/3 müssen wir mit 2 erweitern, um 6 als Nenner zu erhalten:

Wir ersetzen die Rechnung 1/2 + 2/3 im nächsten Schritt mit den erweiterten Brüchen:

2. Schritt: Zähler zusammenrechnen und Nenner stehen lassen!
Hast du die Brüche auf einen gemeinsamen Nenner gebracht, kannst du die Zähler zusammenrechnen, der Nenner bleibt stehen:

3. Schritt: Kürze den Bruch vollständig
Das Ergebnis unseres Beispiels ist 7/6 . Dieser Bruch lässt sich nicht weiter kürzen.
Beispielaufgabe zur Addition von Brüchen
Nutze diese Beispielaufgabe um die Addition zu üben und zum besseren Verständnis

1.) Schritt:
Der kleinste gemeinsame Nenner von 2/6 und 3/5 ist 30.
Der Bruch 2/6 wird mit 5 auf 10/30 erweitert und der Bruch 3/5 wird mit 6 auf 18/30 erweitert.

2.)Schritt:
Die Brüche 10/30 und 18/30 haben beide als Nenner die Zahl 30. Man addiert die Brüche, indem wir die Zähler zusammenrechnen und den Nenner stehen lassen.

3.)Schritt:
Der Bruch 28/30 lässt sich mit zwei kürzen. Es gilt also:

Weitere Übung zum Kürzen
Nutze diese Aufgabe um das Kürzen zu üben und zum besseren Verständnis
Kürze den Bruch 27/9 vollständig.
Gib an, woran man auch ohne zu kürzen erkennt, dass der Bruch größer als 1 ist.
Lösung:
Wir sehen, dass wir den Nenner und den Zähler mit 3 kürzen können.

Der Bruch 9/3 ist noch nicht vollständig gekürzt. Sowohl die 9 im Zähler als auch die 3 im Nenner lässt sich nochmals mit 3 kürzen:

Alternative Lösung:
Anstelle zwei Mal mit der Zahl 3 zu kürzen, könntest du den Bruch 27/9 auch gleich mit 9 kürzen.

Merke: Überlege insbesondere bei großen Brüchen vor dem Kürzen, welche Zahl der größte gemeinsame Vielfache von Zähler und Nenner ist.
Der Bruch 27/9 muss größer als 1 sein, weil der Zähler größer als der Nenner ist.

Die 4 wichtigsten Punkte aus diesem „Mathematik-Lernen“-Beitrag:
- Brüchen sind aus Zähler und Nenner aufgebaut:

- 3 Merkregeln zur Größe eines Bruchs:

- Es gibt 4 Grundrechenarten: Addition (+), Subtraktion (-), Multiplikation (•) und Division (:)
- Addition: Gehe nach der 3-Schritt-Methode vor

Falls du dir die Addition von Brüchen nochmals als Video verdeutlichen möchtest, kannst du das hier tun!
Lade jetzt den Spickzettel zum Thema: “Mathe lernen: Rechnen mit Brüchen – Die Addition” herunter!
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.