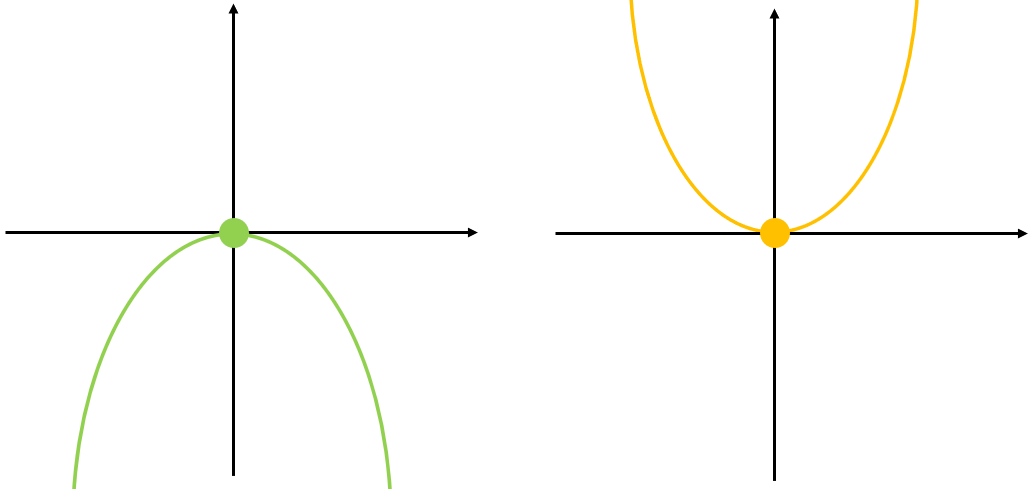Nun kennst du bereits mehrere Eigenschaften von Graphen und weißt wie verschieden sie sein können. Im Matheunterricht berechnet ihr gerade Hoch- und Tiefpunkte und du weißt noch nicht genau wie du dabei vorgehen sollst? Kein Problem, dann ließ dir einfach diesen Blogbeitrag durch und danach wirst du mit Sicherheit einen guten Überblick haben.
Achtung: Du solltest Funktionen fehlerfrei ableiten können. Falls dir das noch nicht gelingt, kannst du hier nochmal alles zum Thema “Ableiten” nachlesen.
Online-Nachhilfe
Erhalte Online-Nachhilfeunterricht von geprüften Nachhilfelehrern mithilfe digitaler Medien über Notebook, PC, Tablet oder Smartphone.
✓ Lernen in gewohnter Umgebung
✓ Qualifizierte Nachhilfelehrer
✓ Alle Schulfächer
✓ Flexible Vertragslaufzeit
Hier noch einmal zur Veranschaulichung:
- Der Graph ist nach unten geöffnet, also ist es ein Hochpunkt (Maximum)
- Der Graph ist nach oben geöffnet, also ist es ein Tiefpunkt (Minimum)
Nun fragst du dich wahrscheinlich, wie man diese bestimmten Punkte berechnen kann, damit man zum Beispiel genau weiß wo sie sich befinden. Dies wird dir anhand eines Beispiels erklärt.
Hochpunkte berechnen
Beispiel: f(x) = x³ – 3x²
1. Schritt: Wir leiten die Funktion zweimal ab.
→ f ‘(x)=3x² – 6x
→ f ”(x)= 6x – 6
2. Schritt: Wir setzten die erste Ableitung gleich 0, denn f´(x)=0 muss gelten. Somit erhalten wir in diesem Fall 2 Punkte und prüfen nun, ob es sich um Hochpunkte oder Tiefpunkte handelt.
f´(x)= 0 → f´(x)= 3x² – 6x =0
= x (3x-6)= 0
X1= 0 und 3x-6=0, also ist x2= 2 (wenn man die Gleichung nach x auflöst)
3. Schritt: Wir setzten die Werte, die wir ausgerechnet haben in die zweite Ableitung ein. Ist das Ergebnis kleiner als null, so hat man ein Maximum. Ist das Ergebnis größer als 0 so erhält man ein Minimum.
f ”(0)= 6⦁0-6= -6 → f ”(x) < 0 → Maximum
f ”(2)= 6⦁2-6= 6 → f ”(x) > 0 → Minimum
4. Schritt: Da wir Hoch-oder TiefPUNKTE berechnen wollen, brauchen wir auch noch einen passenden y-Wert dazu. Den erhält man, indem man den ausgerechneten x-Wert in die gegebene Funktion einsetzt.
→ f(0)= 0 und f(2)= -4
Weiter gehts! Online für die Schule lernen
Lerne online für alle gängigen Schulfächer. Erhalte kostenlos Zugriff auf Erklärungen, Checklisten, Spickzettel und auf unseren Videobereich.
Wähle ein Schulfach aus uns stöbere in unseren Tutorials, eBooks und Checklisten. Egal ob du Vokabeln lernen willst, dir Formeln merken musst oder dich auf ein Referat vorbereitest, die richtigen Tipps findest du hier.