In diesem Teil möchte ich dir zeigen, wie einfach es ist, mit binomischen Formeln zu rechnen. Denn ganz oft haben Schüler das Problem, du ja vielleicht auch, binomische Gleichungen richtig umzuformen oder sogar diese zu erkennen. Die meisten Lehrer versuchen immer, die binomischen Formeln herzuleiten und auf komplizierte Art und Weise zu verdeutlichen. Das ist aber meistens ziemlich verwirrend. Die Folge daraus: Man hört nur die Worte „binomische Formel“ und schon resigniert man. Das sollte so nicht sein, denn es ist so einfach.

Ich möchte dir nun erklären, was es mit den binomischen Formeln auf sich hat und wie man damit ganz einfach rechnen kann.

1. Binomische Formel

Die erste binomische Formel lautet:

Oder noch einfacher:

Aber warum ist das so? Ganz einfach:

Das „hoch 2“ bei (a+b)² bedeutet doch, dass man die Klammer (a+b) mit sich selber multipliziert, denn es heißt ja schließlich auch: x² = x * x

Das würde ja dann heißen:

Wenn du nun diese beiden Klammern ausmultiplizierst erhältst du Folgendes:

Das kann man wiederum zusammenfassen in:

Also hast du nun die erste binomische Formel. Ganz einfach.

Aber was bedeutet das denn jetzt genau?

Angenommen wir haben zwei Strecken – Strecke a und Strecke b.

Diese beiden Strecken addiert man nun und nimmt die Summe zum Quadrat, also genau das, was man bei der ersten binomischen Formel rechnet. (a + b)²

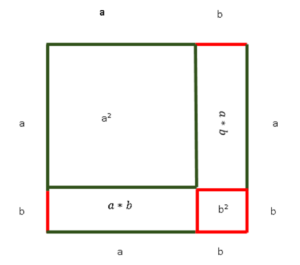
Bildlich dargestellt ergibt das doch ein Quadrat. Eine Strecke die quadriert wird, ergibt nämlich den Flächeninhalt eines Quadrates. A = Seite * Seite. In unserem Fall hat die Strecke eine Länge von (a+b).

Mit der zweiten Binomischen Formel ist es genau so einfach. Wenn du die Erste verstanden hast, wirst du bei der Zweiten keine Probleme mehr haben.

2. Binomische Formel:

Die zweite binomische Formel lautet:

Oder noch einfacher:

Aber warum ist das so? Ganz einfach:

Das „hoch 2“ bei (a-b)² bedeutet doch, dass man die Klammer (a-b) mit sich selber multipliziert, denn es heißt ja schließlich auch: x² = x * x

Das würde ja dann heißen:

Wenn du nun diese beiden Klammern ausmultiplizierst erhältst du Folgendes:

Das kann man wiederum zusammenfassen in:

Also hast du nun die zweite binomische Formel. Ganz einfach.

Du musst dir also im Endeffekt nur die erste Formel merken und wissen, dass in der zweiten binomischen Formel aus dem Plus in der Klammer ein Minus wird, genauso wie aus dem ersten Plus nach dem Gleichzeichen.

So, jetzt hast du auch die zweite Binomische Formel verstanden. Aber, wie du ja weißt, gibt es drei davon. Die dritte Formel ist zwar kürzer und noch leichter zu berechnen, allerdings gibt es hierbei eine große Fehlerquelle: Man muss diese Formel erst einmal in einer Gleichung erkennen. Los geht’s:

3. Binomische Formel

Die dritte binomische Formel lautet:

Oder noch einfacher:

Aber warum ist das so? Ganz einfach:

Man multipliziert diese beiden Klammern einfach aus:

-ab + ab = 0, das heißt, man kann es einfach weglassen. Übrig bleibt: a² – b²

Eigentlich ist das die einfachste binomische Formel, jedoch ist es hier am schwierigsten, diese zu erkennen. Also überlege dir beim Rechnen oder Lösen einer Gleichung oder eines Terms immer ganz genau, ob denn die dritte binomische Formel irgendwo auftaucht.

Wenn du das nicht erkennen solltest, sondern die Klammern dann einfach ausmultiplizierst ist das natürlich nicht schlimm, du würdest einfach nur ein bisschen mehr Zeit brauchen.

Aufgaben Binomische Formeln: